CFA里面的贝叶斯公式在侦破案件时十分有用!!!
学习数学有什么用呢?
高大上的公式跟我什么关系呢?
它除了是个公式还是个公式呀!
NO!NO!NO!
很多粉丝都是悬疑推理剧的钟爱粉
那你们是否知道
CFA里面的贝叶斯公式
在侦破案件时十分有用!!!
无论是要通过考试还是要成为小侦探
都要来认识一下它
贝叶斯公式简介
所谓的贝叶斯定理源于贝叶斯生前为解决一个“逆概”问题写的一篇文章,而这篇文章是在他死后才由他的一位朋友发表出来的。
在贝叶斯写这篇文章之前,人们已经能够计算“正向概率”,如“假设袋子里面有 N 个白球,M 个黑球,你伸手进去摸一把,摸出黑球的概率是多大”。
而一个自然而然的问题是反过来:“如果我们事先并不知道袋子里面黑白球的比例,而是闭着眼睛摸出一个(或好几个)球,观察这些取出来的球的颜色之后,那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题,就是所谓的逆向概率问题。
全概率公式是求由“某项原因导致某项结果”的概率,而贝叶斯定理则是求“某项结果已知,求是哪项原因导致的”的逆概率,所以贝叶斯定理又叫逆全概率公式。
贝叶斯公式

计算方法
一、概率树的方法
贝叶斯公式(1)的计算画成概率树就是:
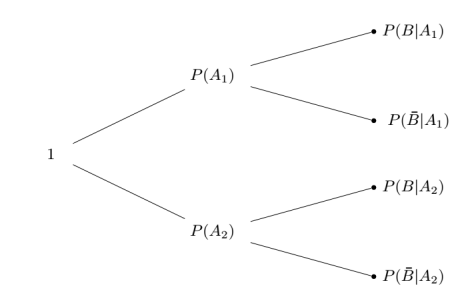
由上图可见,贝叶斯公式的计算就是两层:
(1)第一层的结点数是不定的,考试的题目一般是2到3个。
(2)第二层的是叶子结点也叫终端结点,就是2个(有同学会问,为什么只有2个? 好吧,我等下告诉大家,其实只要画1个。。。)。
(3)为计算清楚,每层结点对齐。
图画到这其实就可以做题目了,这里要告诉大家两个做题技巧。
(1)要分清哪个是结果哪个是“原因”,“原因”是第一层的结点,“结果”是第二层的终端结点,有同学说很难区分,汗。。。我只能说,题目要我们求的概率可以看成是“原因”,至于“结果”嘛,就是该“原因”导致的啦,一般题目提问的话里就包含说的“结果”和“原因”了。
(2)如果是计算事件B发生了,那么所有出B的结点全部忽略。
如果是计算事件B发生了,那么所有出现B的结点全部忽略。
那么概率树可以简化为下图:
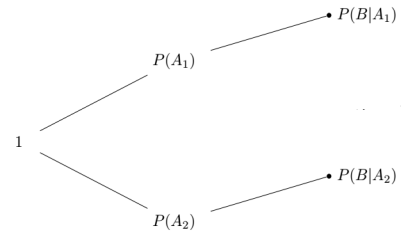
看到没有,就是两层,而且最后一层每个终端节点只有1个!也就是那些补集的概率根本不要去算!直接上个例题。
例题:一机器在良好状态生产合格产品几率是90%,在故障状态生产合格产品几率是30%,机器良好的概率是75%,若一日第一件产品是合格品,那么此日机器良好的概率是多少。
解:看题目我们知道题目最后一句中“若”字代表的是结果,那结果就是“产品合格”,求的是“机器良好的概率”,那么这就是要求的“原因”的概率了。没什么好说的,直接画图:
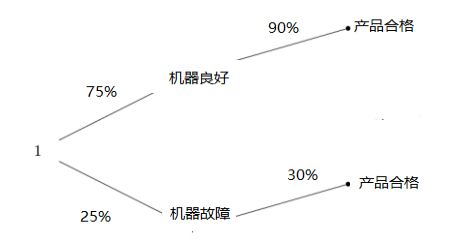
由上图我们可以很清楚的知道“产品合格”这个“结果”是“机器良好”这个原因产生的概率为:
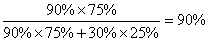
在实际计算,我喜欢在公式分子分母中省去百分号,这样书写方便点。啰嗦很多,如果大家仔细体会,会发现用我说的概率树方法求贝叶斯公式一点也不难。
二、田字格的方法
我们先把田字格图画出来:
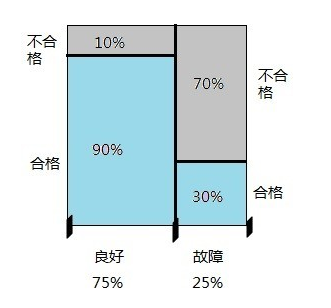
题目所求的此日机器良好的概率就是左下角的那个蓝色方格的面积占蓝色部分的面积的比例,是不是也很清楚?
不管是概率树还是田字图,其实计算过程是一样的,简化概率树也可以看成是在求田字图的面积。这里关键还是要分清什么是“结果”,什么是“原因”,一般就在题目中的提问的话里找。